Grundkonstruktionen
(Arbeitsabläufe, einfachere Variante)

Konstruktion eines Kreises (Teil I)
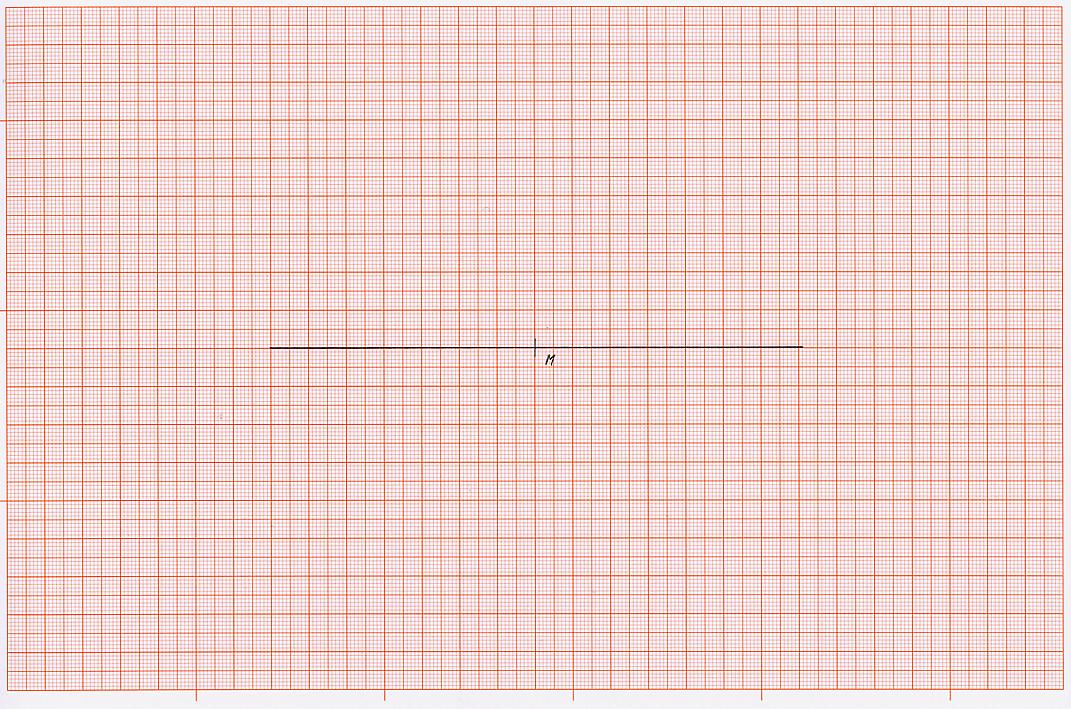
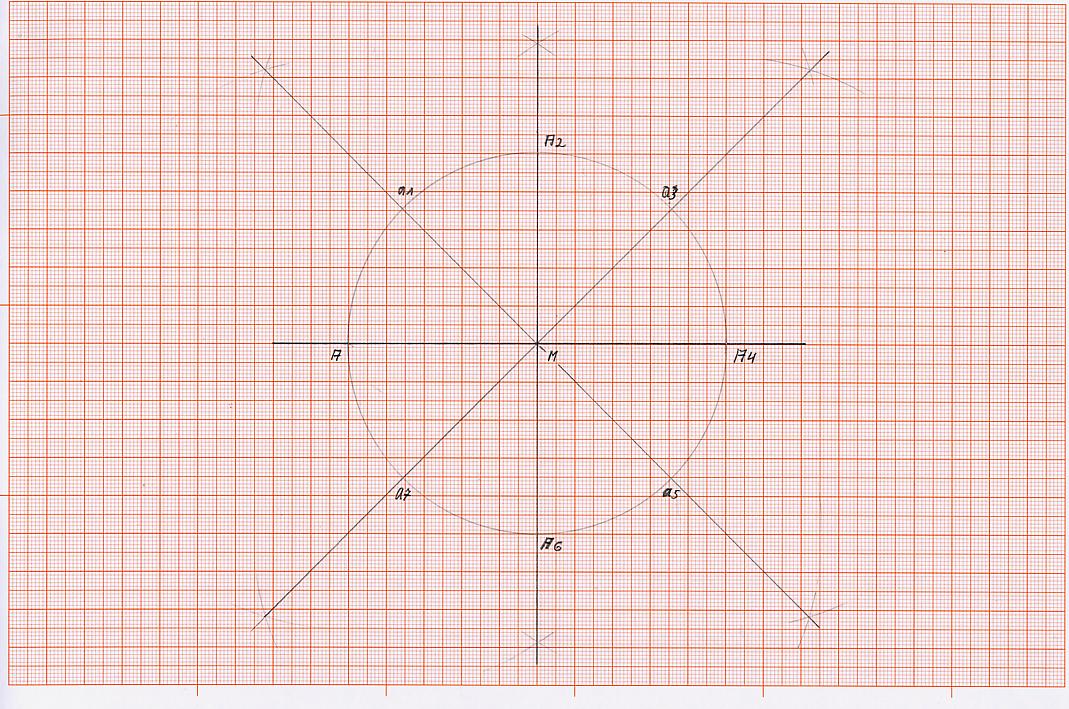
K 1) zeichne eine waagerechte Linie

K 2) lege z. B. in der Mitte auf der Linie einen Punkt fest und bezeichnen ihn mit „M“ (Mittelpunkt).

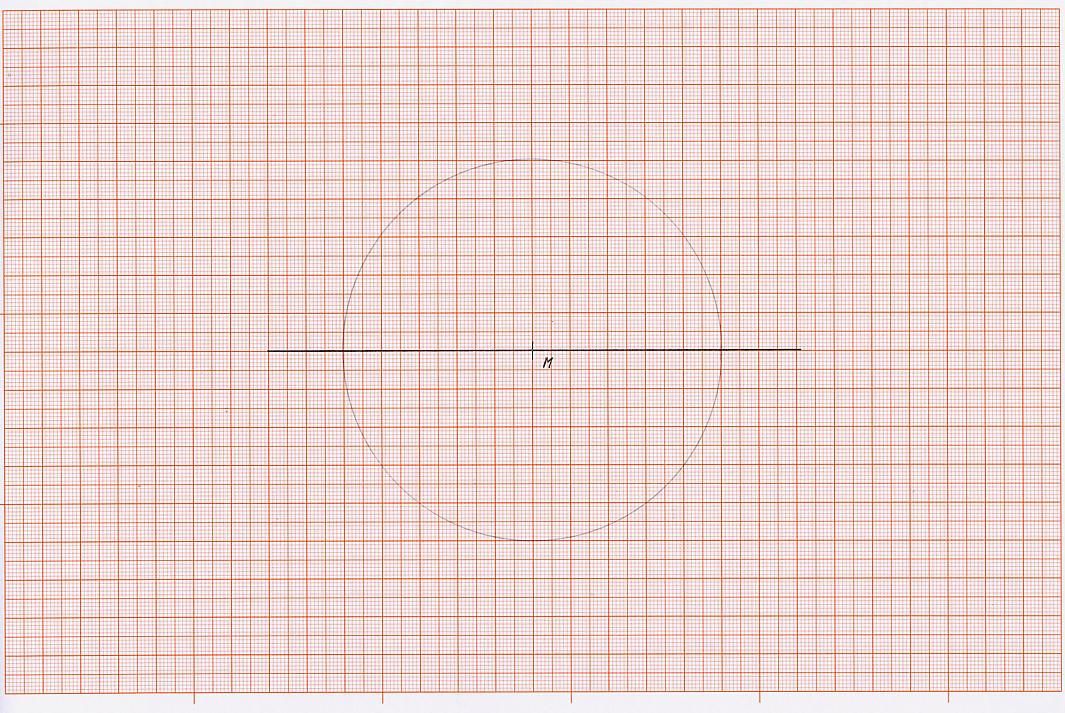
K 3) schlagen mit einer gewünschten Zirkelöffnung um den Punkt M einen Kreis und erhalte dann den gewünschten Kreis.

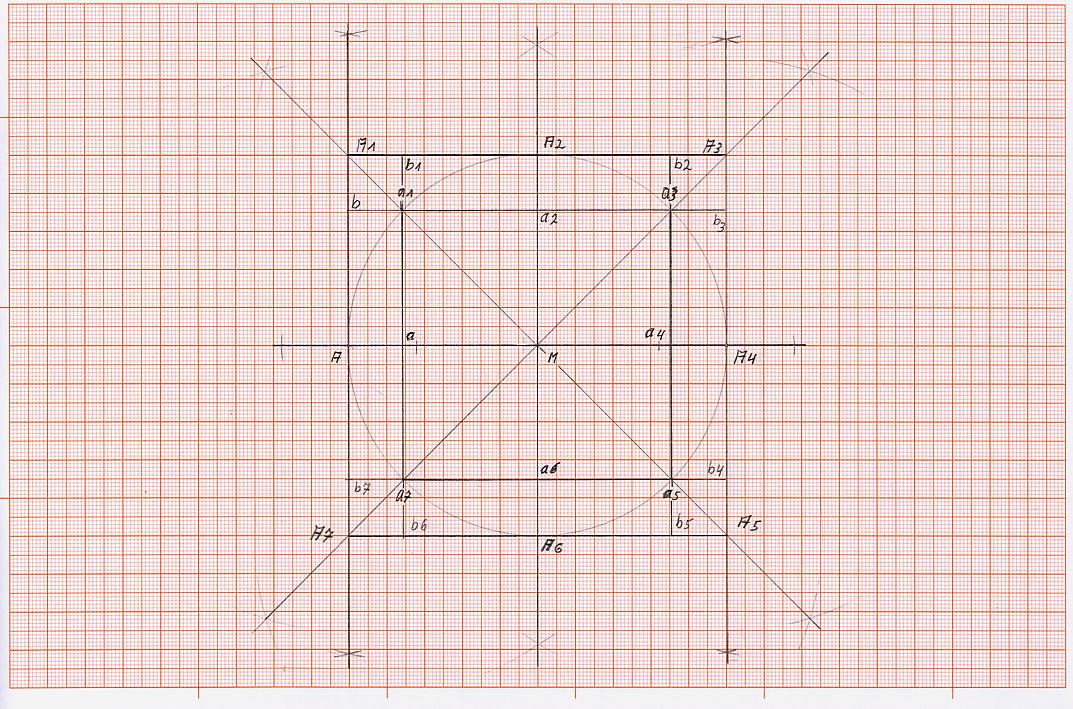
Grundkonstruktion für die Quadratur des Kreises (Teil II)

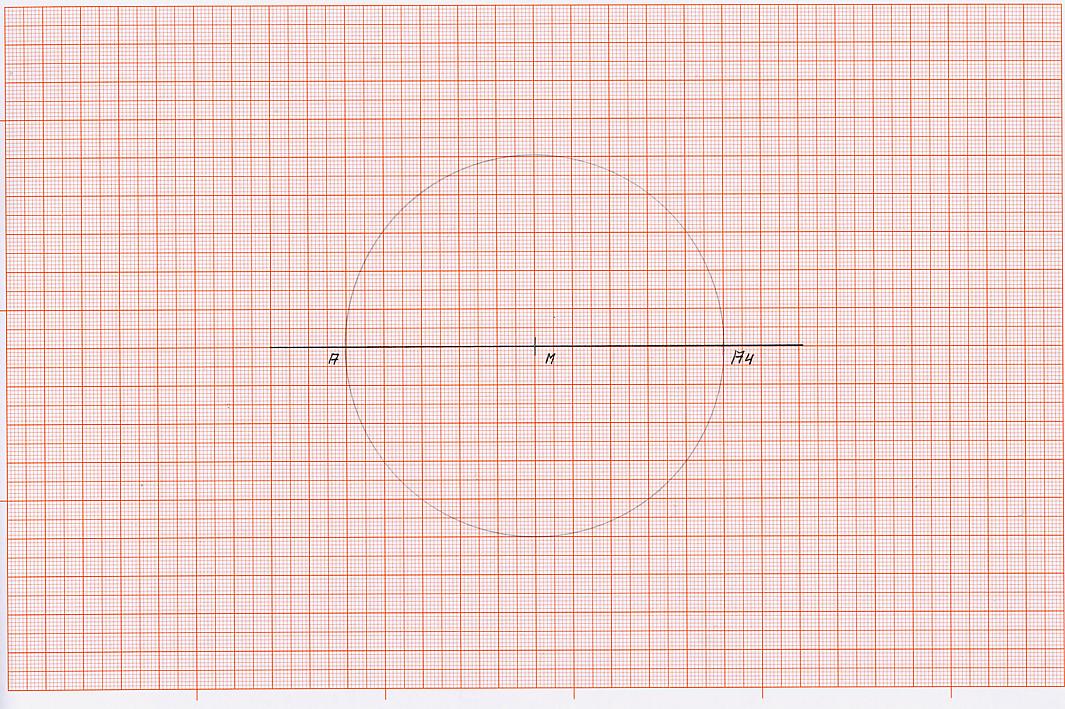
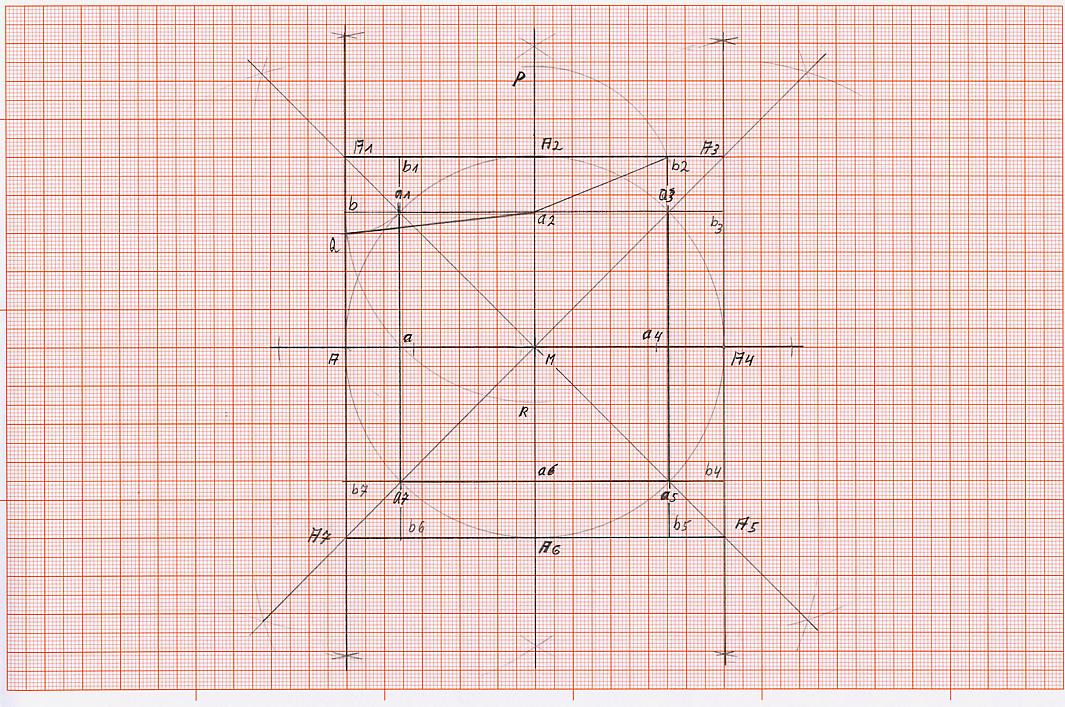
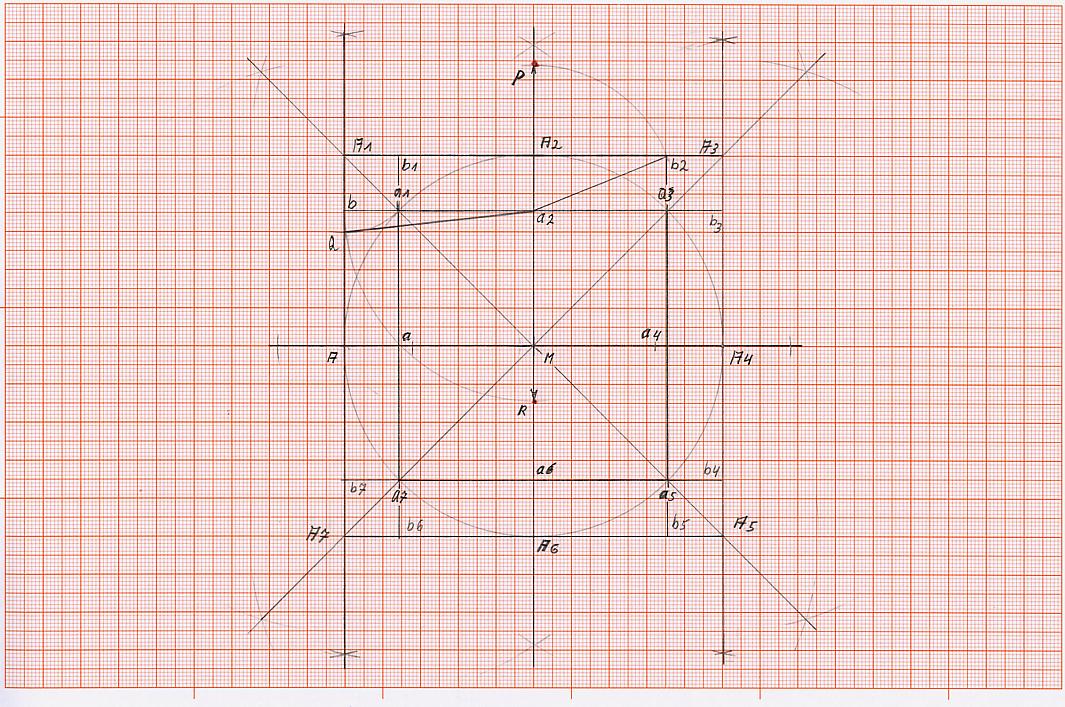
K 1) zeichne durch den Mittelpunkt “M“ eine waagerechte Linie (wenn nicht schon durch die Kreiskonstruktion vorgegeben), sodass sie den Kreis links im Punkt A und rechts im Punkt A4 schneidet.

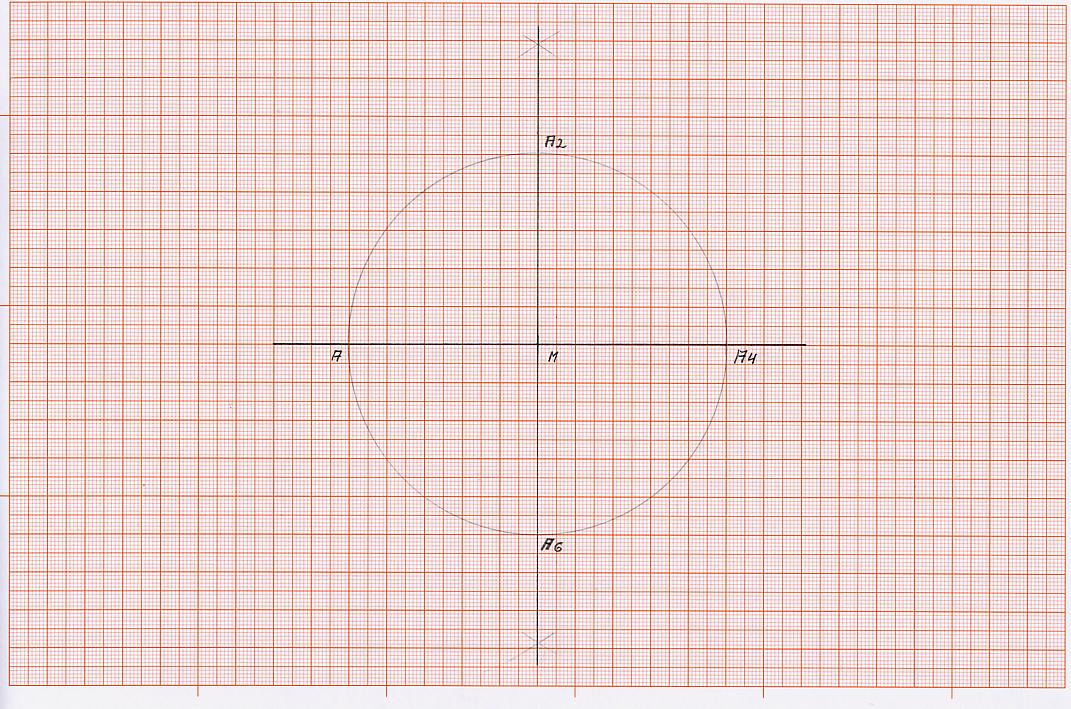
K 2) errichte im Punkt “M“ eine Senkrechte, sodass der Kreis oben im Punkt A2 und unten im Punkt A6 geschnitten wird.

K 3) halbiere die Winkel MA – MA2, MA2 – MA4, MA4 – MA6, MA6 – MA und erhalte jeweils dort, wo die Winkelhalbierende die Kreislinie schneidet, die Schnittpunkte a1, a3, a5 und a7.

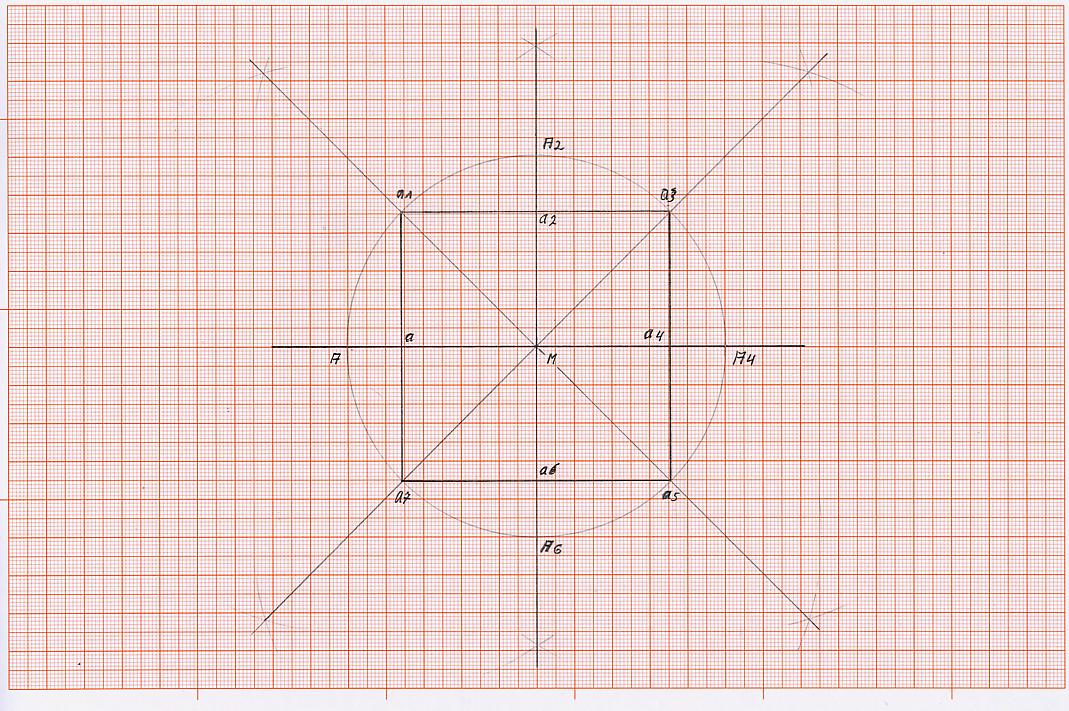
K 4) konstruiere das innere Quadrat, in dem die Punkte a1 mit a3, a3 mit a5, a5 mit a7 und a7 mit a1 miteinander verbunden werden. Hierbei erhalten wir noch, in dem wir die waagerechte durch Punkt M geführte Strecke schneiden, die Schnittpunkte a und a4, außerdem durch das schneiden der durch Punkt M geführten senkrechten Strecke, die Schnittpunkte a2 und a6.

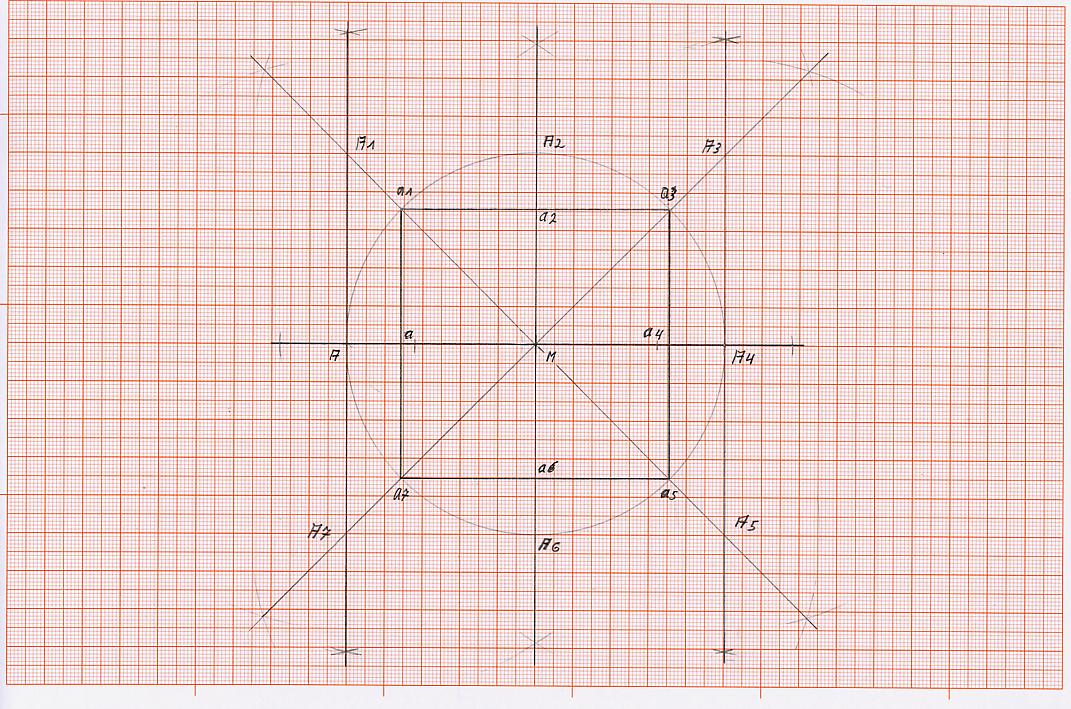
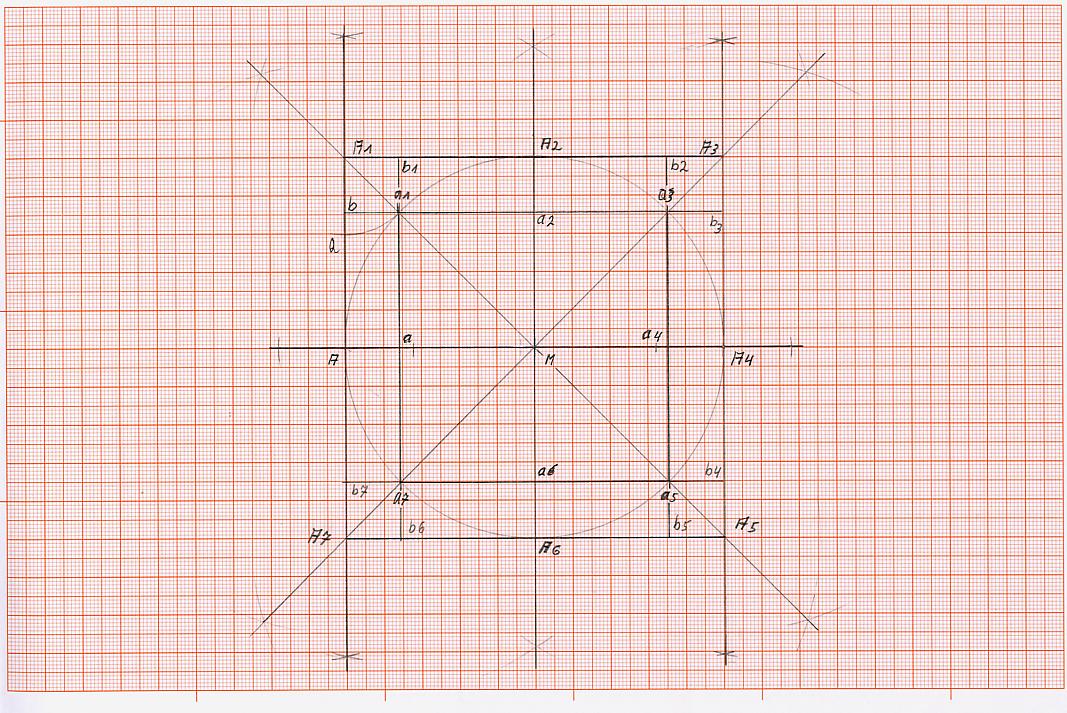
K 5) konstruierte das äußere Quadrat, in dem jeweils in den Punkten A und A4 eine Senkrechte errichtet wird, die so zu verlängern ist, dass sie die Linie, die von M über a1 hinaus geführt wird, in Punkt A1, die Linie, die von M über a3 hinausgeführt wird, in Punkt A3, die Linie, die von M über a5 hinausgeführt wird, in Punkt A5, die Linie, die von M über a7 hinausgeführt wird in Punkt A7 schneidet.

K 6) Jetzt müssen nur noch die Punkte A1 mitA3 und A5 mit A7 verbunden werden, um das äußere Quadrat vollständig zu erstellen. Hierbei erhalten wir noch, in dem wir die waagerechte durch Punkt M geführte Strecke schneiden, die Schnittpunkte A und A4, außerdem durch das schneiden der durch Punkt M geführten senkrechten Strecke, die Schnittpunkte A2 und A6.

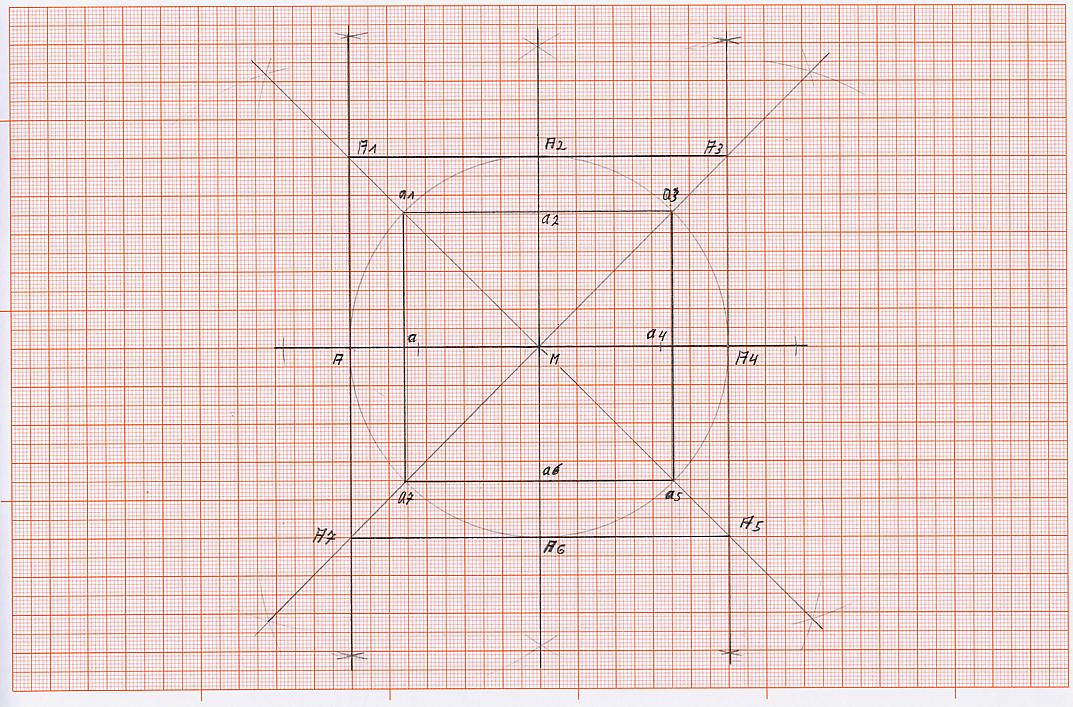
K 7) Wenn jetzt auch noch die Seiten des inneren Quadrats soweit verlängert werden, dass sie die Seiten des äußeren Quadrats schneiden, entstehen die Schnittpunkte b, b1, b2, b3, b4, b5, b6, b7.

Nun ist die Grundkonzeption, die für weiteres Vorgehen benötigt wird, fertiggestellt.

Weiterführende Konstruktionen (Teil III)

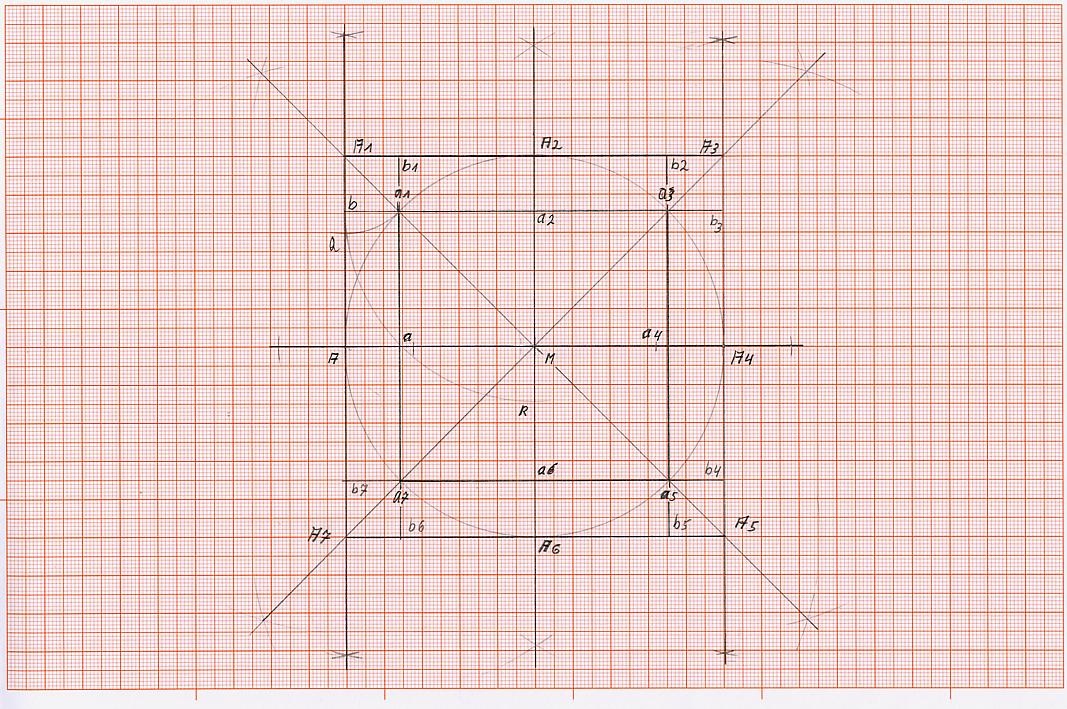
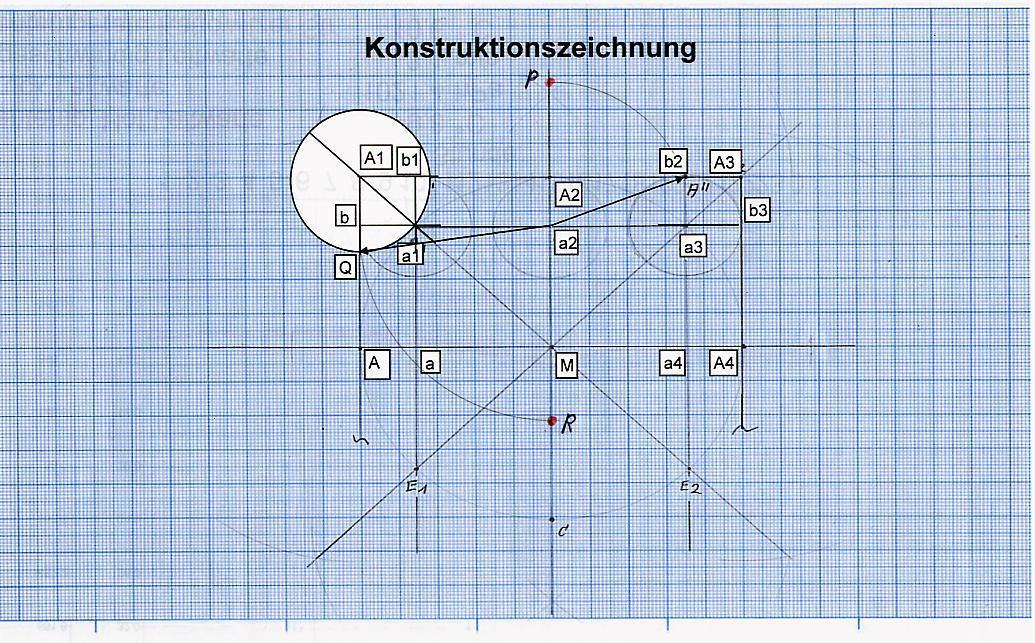
K 1) Schlage um den Punkt A1 einen Kreisbogen mit dem Radius A1a1, wobei dieser Kreisbogen die Strecke bA in dem Punkt Q schneidet. Es entsteht die Strecke a2Q.

K 2) nehmen die Strecke a2Q in den Zirkel und schlage um den Punkt a2 einen Kreisbogen, sodass er die Strecke die von a2 ausgehend über den Punkt M hinausgeführt worden ist, also die Strecke Ma6, im Punkt R schneidet.

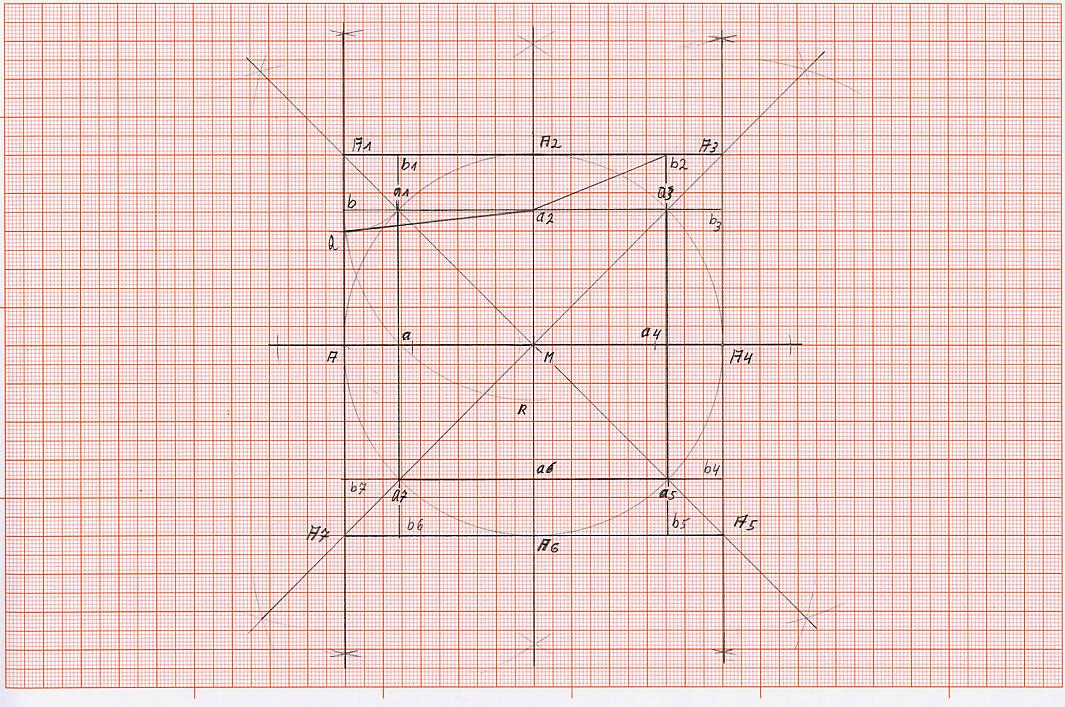
K3) Verbinde nun die Punkte a2 und Q, es ist die Strecke a2Q entstanden. Verbinde auch a2 und b2, somit ist die Strecke a2b2 entstanden.

K4) schlage um den Punkt a2 mit der Strecke a2b2 einen Kreisbogen, der von Punkt M über die Punkte a2 und A2 hinausgehend die Linie, in Punkt P schneidet.

K5) die neue Strecke RP entspricht mit relativ guter Genauigkeit der Kantenlänge des Quadrats, das den gleichen Flächeninhalt hat, wie der vorgegebene Kreis.

Die Strecke PR entspricht ziemlich genau der Kantenlänge des gesuchten Quadrats.

Berechnungen bei Ausführungen nach der Grundkonstruktion

Annahme Kreisdurchmesser D = 100 mm

Entstehung und Berechnung der Strecke: von a2 nach Q
Schlage um A1 einen Kreis mit dem Radius A1a1
wo dieser Kreisbogen die Linie bA1 schneidet entsteht der Schnittpunkt „Q“
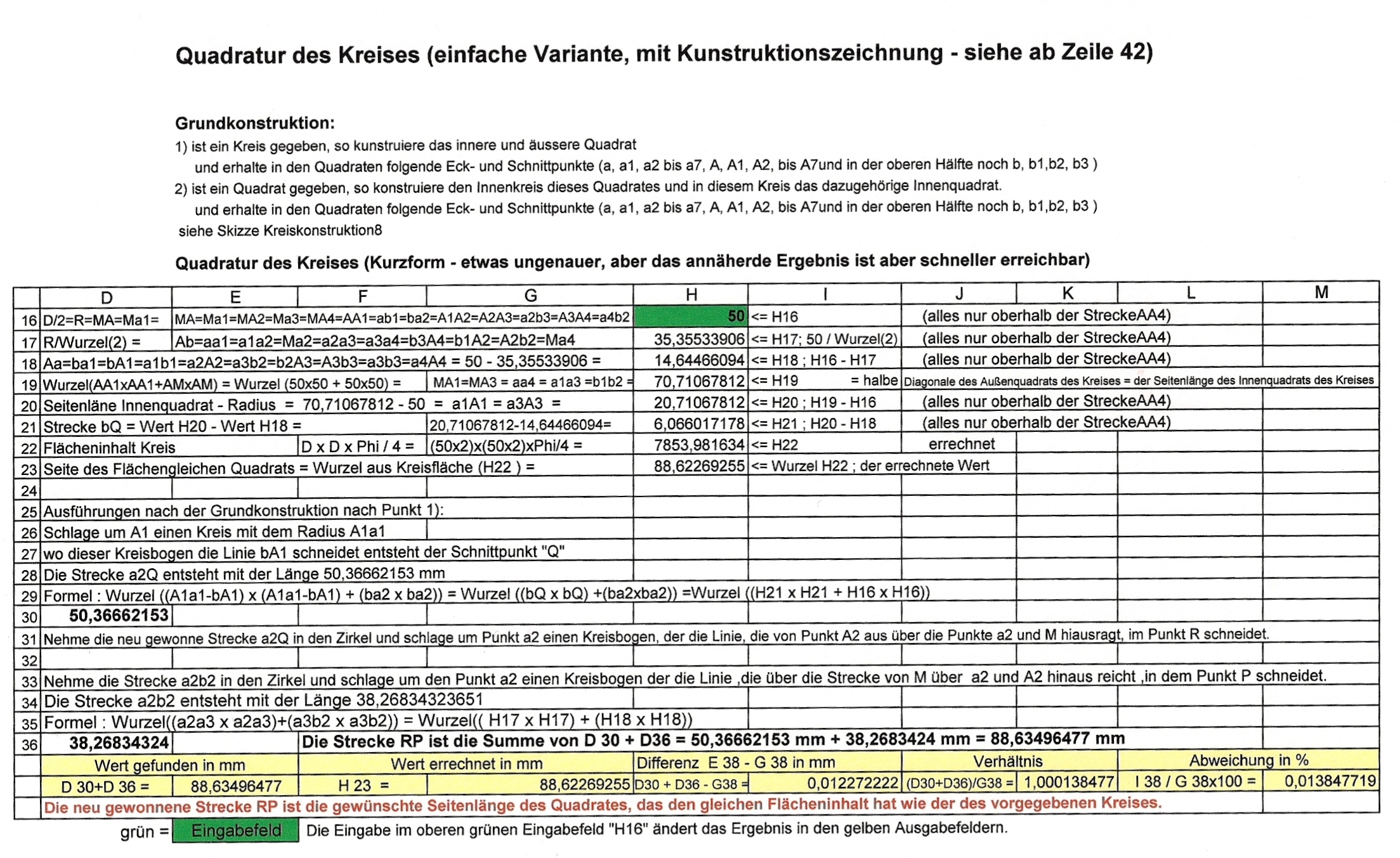
Die Strecke a2Q entsteht mit der Länge 50,36662153 mm
Formel : Wurzel ((A1a1-bA1) x (A1a1-bA1) + (ba2 x ba2)) = Wurzel ((bQ x bQ) +(ba2xba2)) =Wurzel ((H21 x H21 + H16 x H16))
50,36662153 mm
Entstehung und Berechnung der Strecke: von a2 nach b2
Nehme die Strecke a2b2 in den Zirkel und schlage um den Punkt a2 einen Kreisbogen der die Linie ,die über die Strecke von M über a2 und A2 hinaus reicht ,in dem Punkt P schneidet.
Die Strecke a2b2 entsteht mit der Länge 38,26834323651
Formel : Wurzel((a2a3 x a2a3)+(a3b2 x a3b2)) = Wurzel(( H17 x H17) + (H18 x H18))
38,2683424 mm
Die Strecke RP ist die Summe von D 30 + D36 = 50,36662153 mm + 38,2683424 mm = 88,63496477 mm.

Die Seitenlänge des Quadrats mit dem gleichen Flächeninhalt wie der des vorgegebenen Kreises beträgt gemäß der Konstruktion: 88,63496477 mm

Die Seitenlänge des Quadrats mit dem gleichen Flächeninhalt wie der des vorgegebenen Kreises beträgt errechnet : Wurzel aus (D2 x Phi/4) = 88,62269255 mm

Die Differenz von Quadratseite (konstruiert) minus der Quadratseite (errechnet) beträgt:

88,63496477 mm – 88,62269255 mm = 0,012272222 mm

Allgemeingültiger ausgedrückt: Die beiden Quadratseiten stehen in einem Verhältnis von:

Quadratseite (konstruiert) / Quadratseite (errechnet) = 88,63496477 / 88,62269255 =

1,000138477