Die Zahl Pi
Die Zahl entsteht, wenn ich:
1) Einen Kreis mit dem Durchmesser 1 mit dem dazugehörigen inneren Quadrat versehe.
2) Die Seite AB des inneren Quadrats in 5 gleiche Teile zu teilen.
3) Die Strecke A1 (1/5 der Strecke AB) in den Zirkel zu nehmen und mit dieser Länge, um den Punkt A einen Kreisbogen schlage, sodass auf der Strecke AC, die durch den Mittelpunkt des Kreises geht, der Punkt F entsteht.
4) Zu der Strecke AF , die der Länge von 1 / 5 der Seitenlänge der inneren Quadratseite entspricht, 3 x den
Kreisdurchmesser (hier =1) dazu addiere. Also von Punkt A aus, die Strecke des Durchmessers (D) 3 x auf einer Linie, die über die Strecke von Punkt C über Punkt A hinaus gezeichnet wurde, auftrage. Es entsteht der Punkt E.
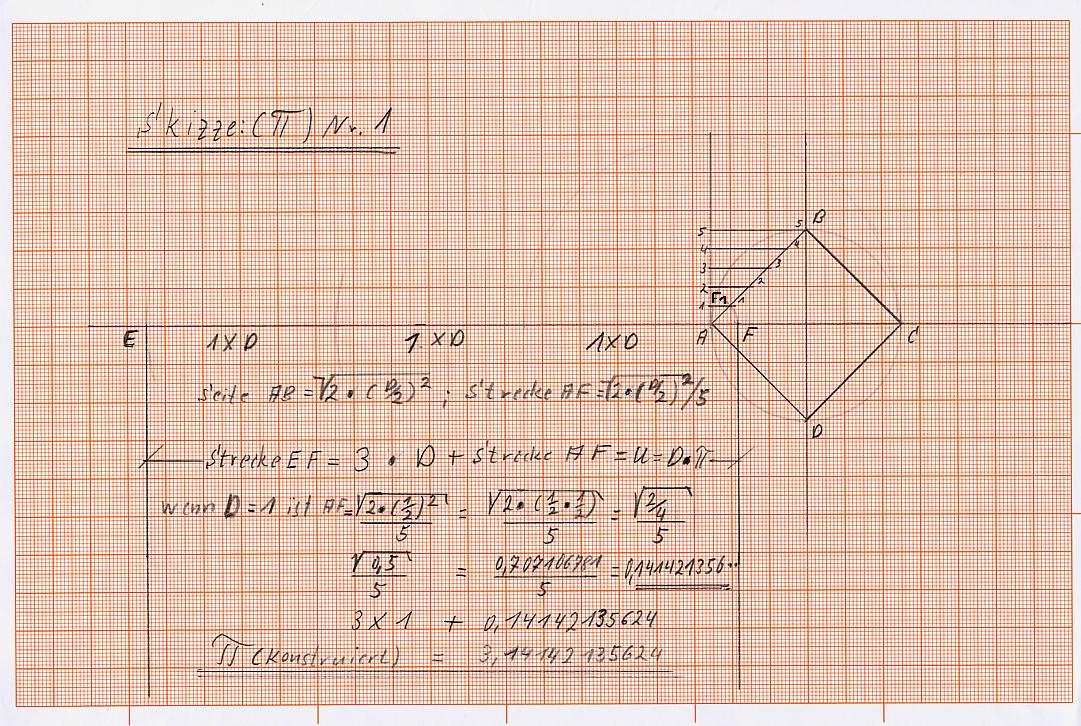
5) Die Strecke E F entspricht mit großer Genauigkeit der Zahl Pi . (Siehe Zeichnung Skizze: (Pi) 1 )
Durchmesser = 1 ; Seitenlänge des Innenquadrats des Kreises mit dem Durchmesser =1 beträgt :1 / Wurzel (2) = 1 : 1, 4142136 = 0,7071068; 1/5 der Seitenlänge des Innenquadrats ist = 0,7071068 / 5 = 0,14142136
3 x den Durchmesser (1 ) und 1 / 5 der Seite des Innenquadrats ( 0,14142136) = 3 x 1 + 0,14142136 = 3,14142136
ist Pi (konstruiert) = 3,14142135624 ; Pi (rechnerisch) = 3,14159265359 ;
Differenz der beiden Werte (Pi rechnerisch) – Pi (konstruiert) = 3,14159265359 – 3,14142135624 = 0,0001712935
Umfang des Kreises
Der Umfang des Kreises wird ermittelt, indem man dreimal den Durchmesser des gegebenen Kreises an die Strecke AF
( 1 / 5 der Seitenlänge des inneren Quadrats dieses Kreises) addiert. (Siehe Zeichnung Skizze: (Pi) 1 )
oder:
Der Umfang des Kreises wird ermittelt, in dem man dreimal den Durchmesser des Kreises an die Strecke 01
( 1 / 5 der Seitenlänge des inneren Quadrats dieses Kreises) addiert. (Siehe Zeichnung Skizze: (Pi) 2 )
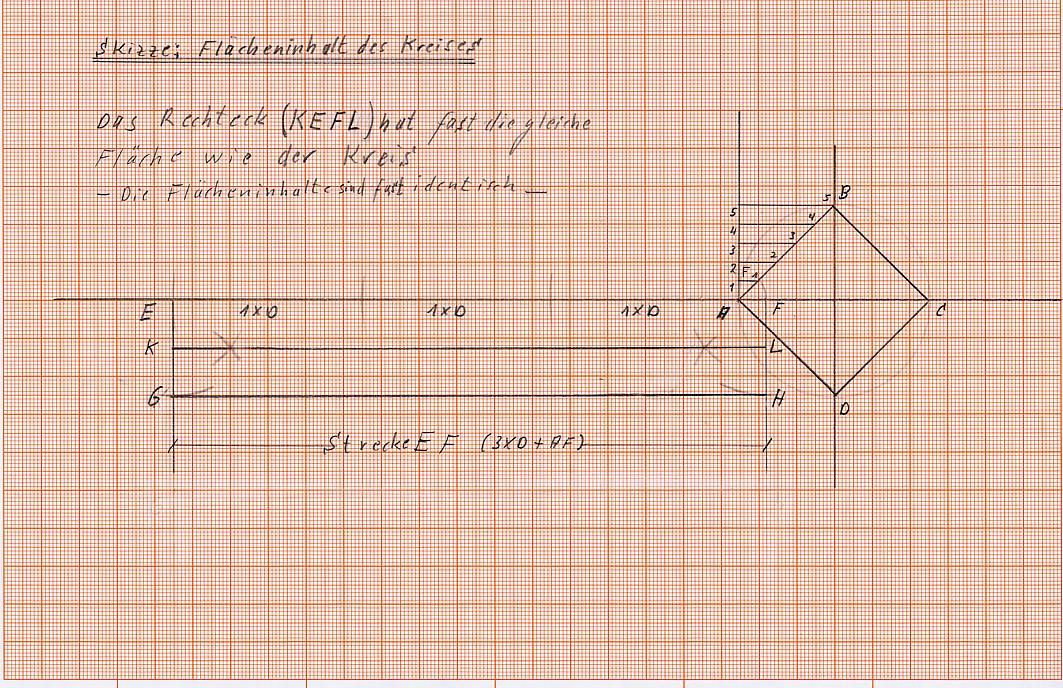
Flächeninhalt des Kreises
Der Flächeninhalt des Kreises wird ermittelt, indem man dreimal den Durchmesser des gegebenen Kreises an die Strecke AF oder A1 (beide haben die gleiche Länge = 1 / 5 der Seite des Innenquadrats oder 1 / 10 der Diagonale des Außenquadrats) addiert und diese gefundene Länge, mit der Strecke EF die = D/4 (einem Viertel der Länge des Durchmessers) ist, multipliziert.
Dies geschieht, in dem man in den Punkten E und F je eine Senkrechte errichtet und um die Punkte E und F einen Kreisbogen mit dem Radius des Kreises (D / 2) schlägt. Die neuen Punkte nennt man G und H. Dann werden die Strecken EG und FH halbiert und ich gewinne die Punkte K und L .Nun wird eine Parallele zur Strecke EF durch die Punkte K und L gezogen.
Oder man nimmt gleich die Länge D/4 (1/4 Durchmesser) in den Zirkel und schlägt mit dieser Länge je einen Kreisbogen um die Punkte G und H, sodass ohne Umwege die Punkte K und L entstehen. Das Rechteck mit den Endpunkten K, E, F, L hat den gleichen Flächeninhalt wie die Kreisfläche mit dem Durchmesser D. (siehe Skizze: Flächeninhalt des Kreises)
Weitere Konstruktionsmöglichkeiten:
Für den Flächeninhalt des Kreise: Die Strecke D/4 (1/4 Durchmesser) entsteht auch, wenn ich die Strecke AM halbiere.
Die Zahl Pi entsteht, auch wenn ich:
1) Einen Kreis mit dem Durchmesser 1 mit dem dazugehörigen inneren Quadrat versehe.
2) Die Seite AB des inneren Quadrats schneidet die waagerechte Linie, die durch den Kreismittelpunkt geht, im Schnittpunkt 0 .
3) Die Strecke 0E, die der Länge der Seiten des inneren Quadrats entspricht, ist in 5 gleiche Teile zu teilen.
4) Zu der Strecke 01 , mit der Länge von 1 / 5 der Seitenlänge der inneren Quadratseite, sind 3 x der Kreisdurchmesser (hier =1) zu addieren.
5) Die Strecke A1 B1 entspricht mit großer Genauigkeit der Zahl Pi . (Siehe Zeichnung Skizze: (Pi) 2 )
oder:
1) Einen Kreis mit dem Durchmesser 1 mit dem dazugehörigen äußeren Quadrat versehen.
2) Die Diagonale des äußeren Quadrats in 10 gleiche Teile teilen (oder die halbe Diagonale, die der Seite des inneren Quadrats entspricht, in fünf gleiche Teile teilen. Der zehnte Teil der Diagonale des äußeren Quadrats entspricht dem fünften Teil der halben Diagonale oder gleich dem fünften Teil der Seite des inneren Quadrats).
3) zu der Strecke (ein Zehntel der Diagonale des äußeren Quadrats oder entsprechend des 5. Teils der Seite des inneren Quadrats) noch dreimal den Durchmesser des Kreises (oder sechsmal den Radius des Kreises) addiere.
4) die gesuchte Gesamtstrecke entsteht: aus 3 mal den Durchmesser des Kreises (6 mal den Radius des Kreises) und einem Zehntel der Diagonale des äußeren Quadrats (oder ein Fünftel der Seite des inneren Quadrats).
Hierzu sind weitere Aussagen aus den beigefügten Zeichnungen zu ersehen.
Dazu zwei selbsterklärende Zeichnungen.
Es gibt eine noch genauere, aber auch aufwendiger Konstruktion. Dazu ist der Autor zu konsultieren.
Die Strecke E – X entspricht dann recht genau der Zahl Pi.
Pi (errechnet): 3,14159265358979, Pi (konstruiert): 3,1415926629547
————————————————————
Differenz: 0, 00000000936492
=================================