Konstruktion der Seite eines Quadrats, 

das den gleichen Flächeninhalt hat wie der des vorgegebenen Kreises. 

( nach der einfachen Pi Ermittlung )

Zu erst die Grundkonstruktionen

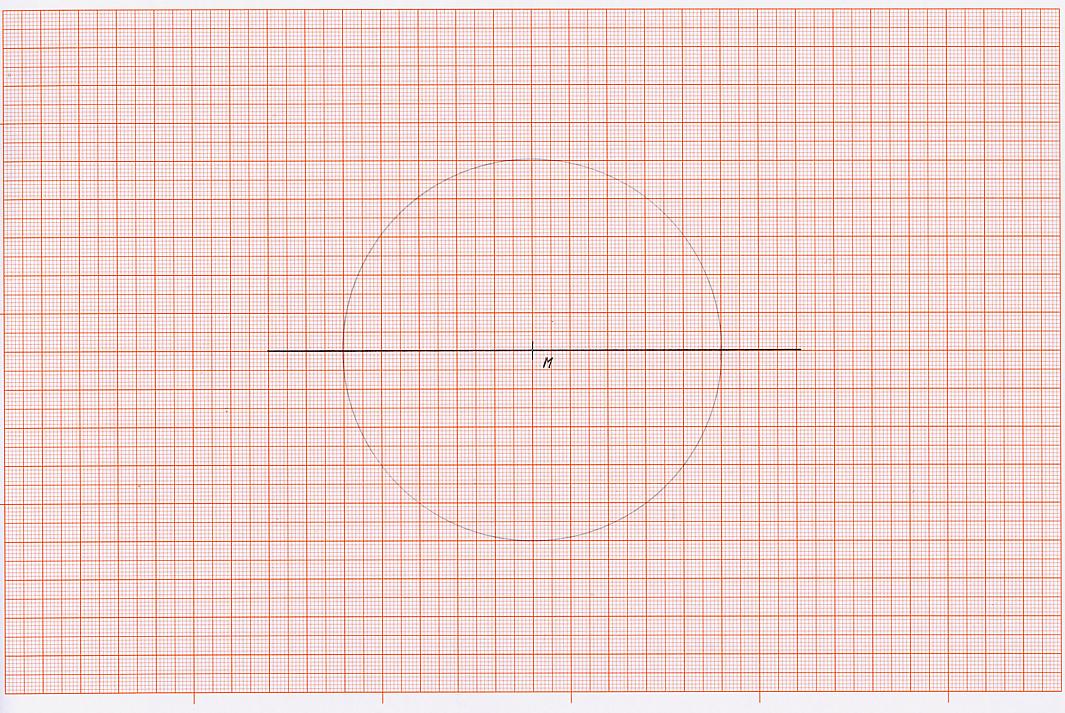
(Siehe Konstruktion eines Kreises (Teil I), mit folgendem Ergebnis)

 

Nun weiterführende neue Konstruktionsschritte:

Dann wird weiter ausgeführt (Teil II)

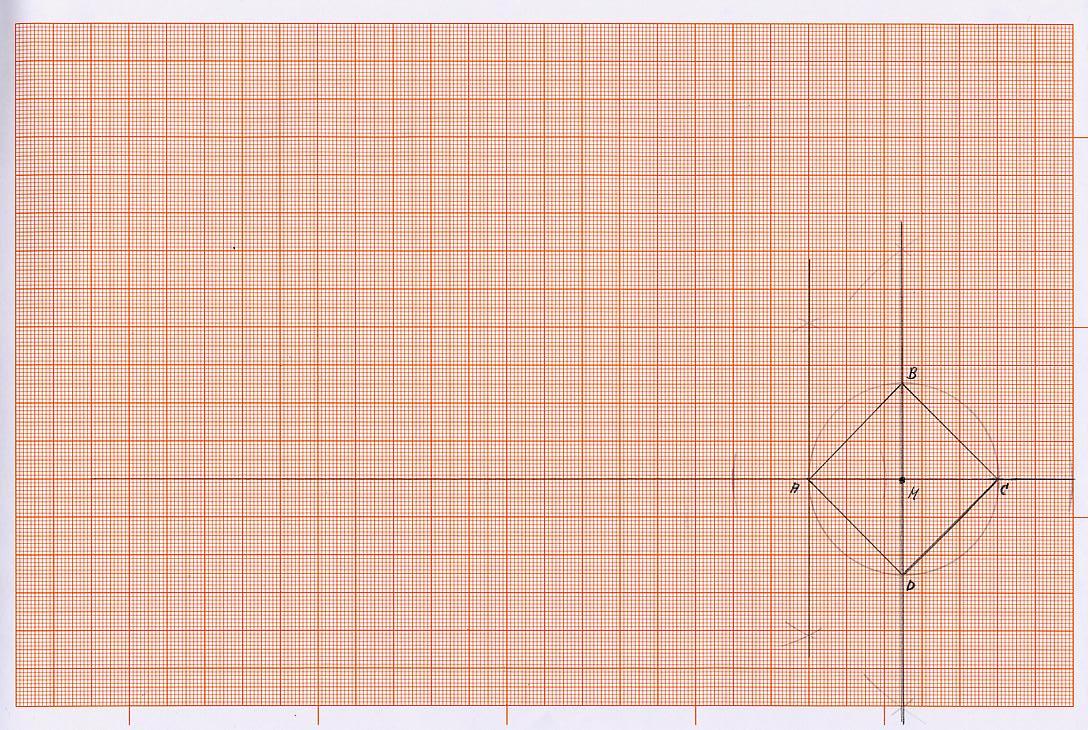
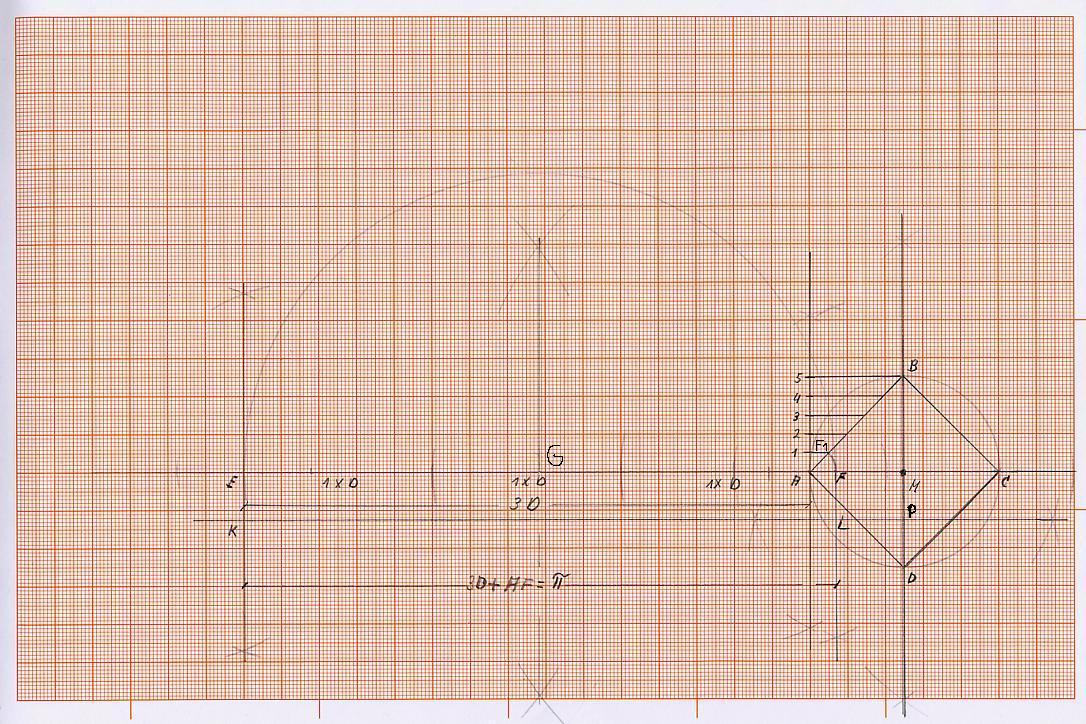
K1) Die Seite des Quadrats, das den gleichen Flächeninhalt hat wie der des vorgegebenen Kreises, erhalte ich, in dem man in dem vorgegebenen Kreis das innere Quadrat mit den Punkten A B C D zeichnet (als weitere Grundkonstruktion).

 

K2) Wir ziehen dann jeweils eine Linie, die über den Punkt D, den Mittelpunkt des Kreises M und den Punkt B hinausgeht und eine Linie, die von dem Punkt C über den Punkt M, den Mittelpunkt des Kreises, über den Punkt A hinausgeht. Nun trage ich auf der Linie, die von Punkt C über den Punkt M und A hinausgeht, vom Punkt A aus dreimal den Durchmesser des Kreises auf und erhalte den Punkt E.

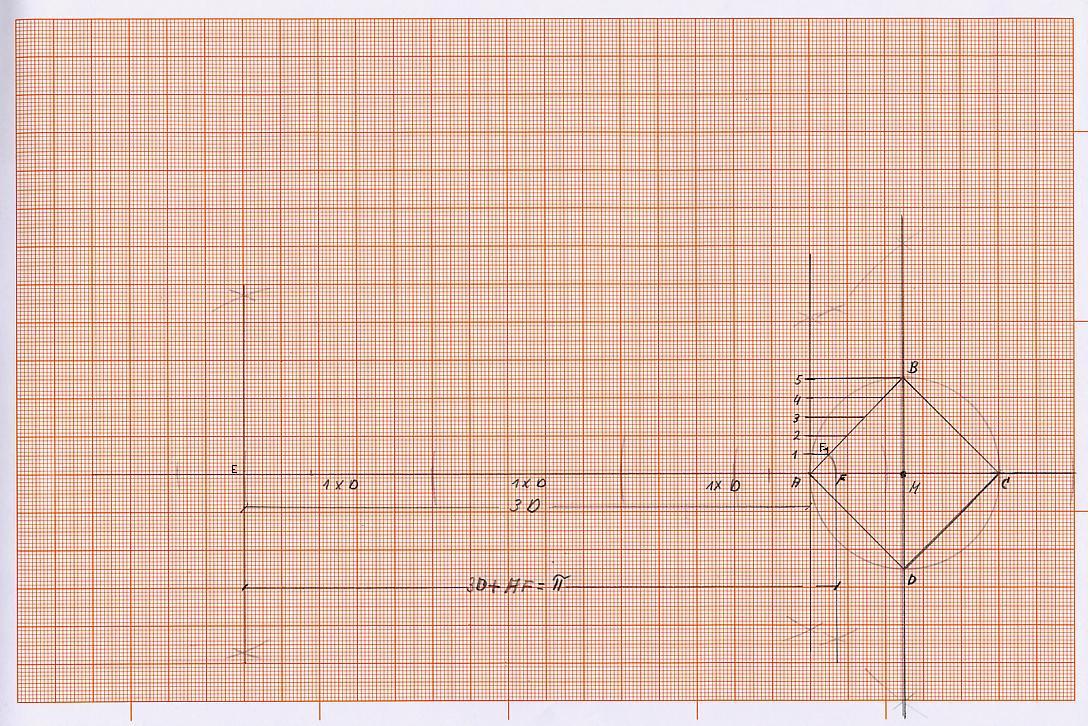
Errichte in Punkt A eine Senkrechte, auf der ich 5gleiche Teilstrecken auftrage. Die Seite des inneren Quadrats mit den Endpunkten A und B teile ich nun mittels des Strahlensatzes in fünf gleiche Teile.

Jetzt schlage ich um Punkt A einen Kreisbogen mit der Strecke A F1, die ein Fünftel der Seite des inneren Quadrats mit den Endpunkten A B entspricht und schneidet die Strecke A M im Punkt F.

Die Strecke A F entspricht der Strecke A F1 und ist ein Fünftel der Länge einer Seite des inneren Quadrats. Errichte jeweils in den Punkten F und E eine Senkrechte.

 

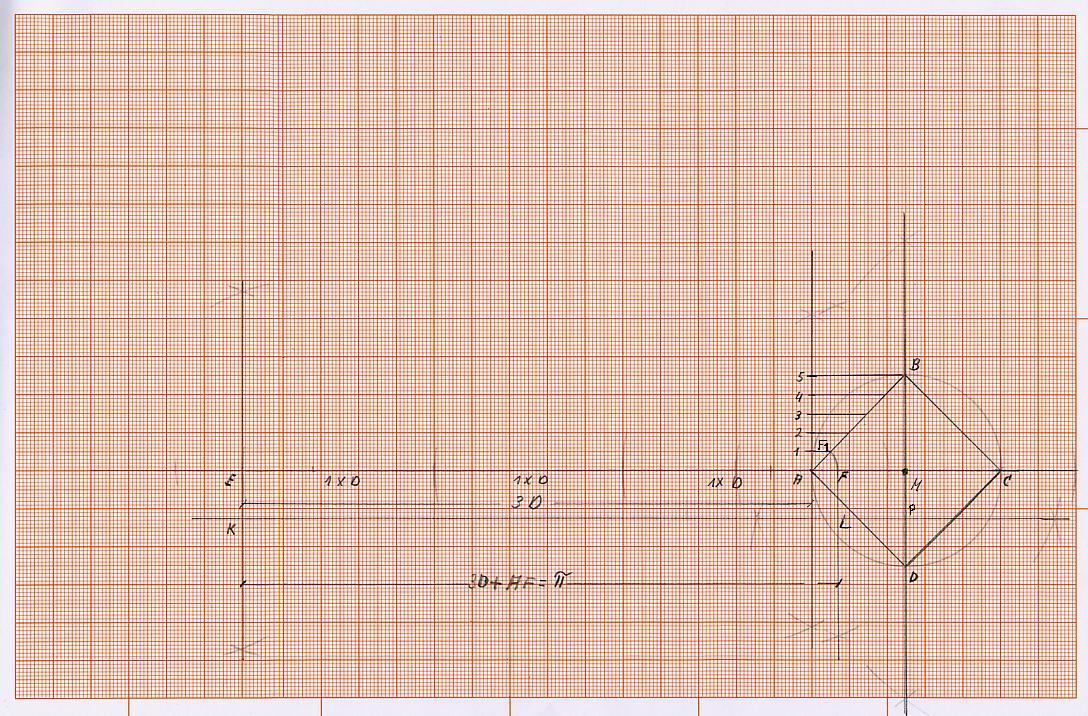
K3) Halbiere jetzt die Strecke (M D) und erhalte den Punkt P. Schlage um den Punkt F und um den Punkt E mit der Strecke MP einen Kreisbogen. Die Senkrechte, die in Punkt F errichtet und auch senkrecht nach unten verlängert wurde, wird im Punkt L und die Senkrechte, die im Punkt E errichtet und auch senkrecht nach unten verlängert wurde, wird im Punkt K geschnitten. Verbinde die Punkte K und L. Es entsteht das Rechteck EFLK, das den gleichen Flächeninhalt hat wie der vorgegebene Kreis (die Ausgangsgröße).

 

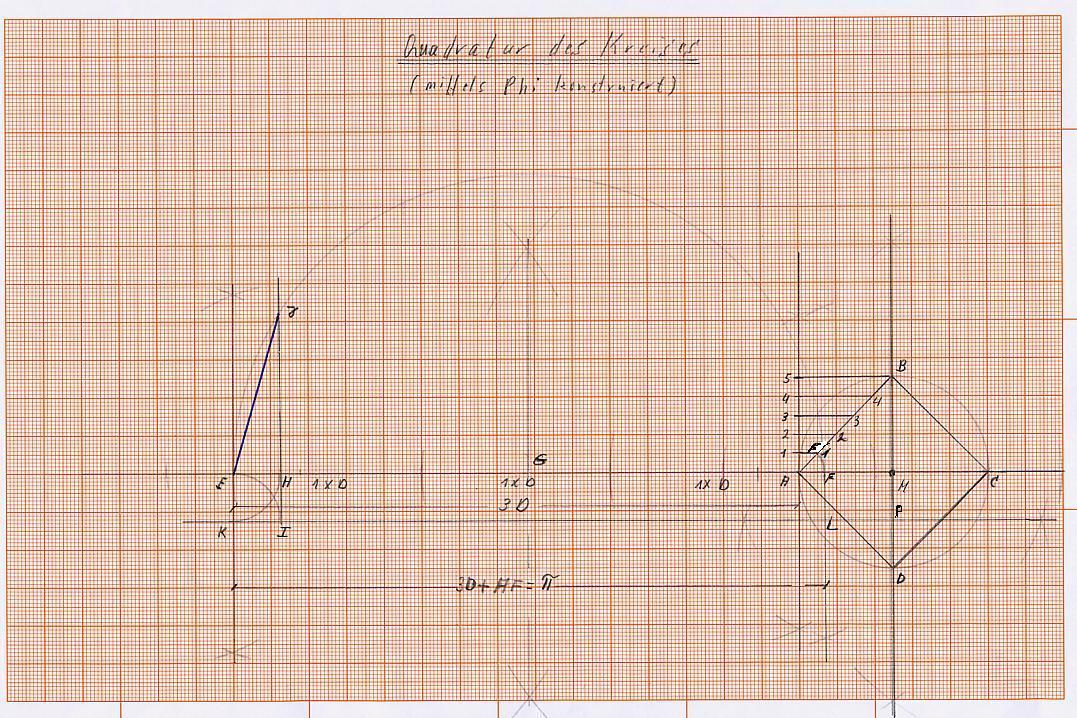
K4) Halbiere jetzt die lange Seite (E F) des Rechtecks mit den Endpunkten E F L K und finde den Punkt G. Schlage nun mit der halben Länge der Seite E F, also mit der Strecke E G, einen Kreisbogen um Punkt G, also von dem Punkt E zu dem Punkt F.

 

K5) Schlage dann um den Punkt E und um den Punkt K jeweils einen Kreisbogen mit der Länge der kürzeren Seite, hier mit der Strecke E K (siehe Skizze) und finde beim Schneiden der Strecken EA und KL die Punkte H und I. Verbinde den Punkt I mit dem Punkt H und führe die Linie über den Punkt H hinaus, bis sie den Kreisbogen über die Strecke EF in dem Punkt J schneidet (oder errichte im Punkt H eine Senkrechte, bis diese unten den Punkt I schneidet und den Kreisbogen im Punkt J).

Die Verbindungslinie der Punkte E J, also Strecke E J, ist die gesuchte Seitenlänge des Quadrats, das die gleiche Fläche hat wie die des vorgegebenen Kreises.

Strecke E J, ist die gesuchte Seitenlänge des Quadrats.

 

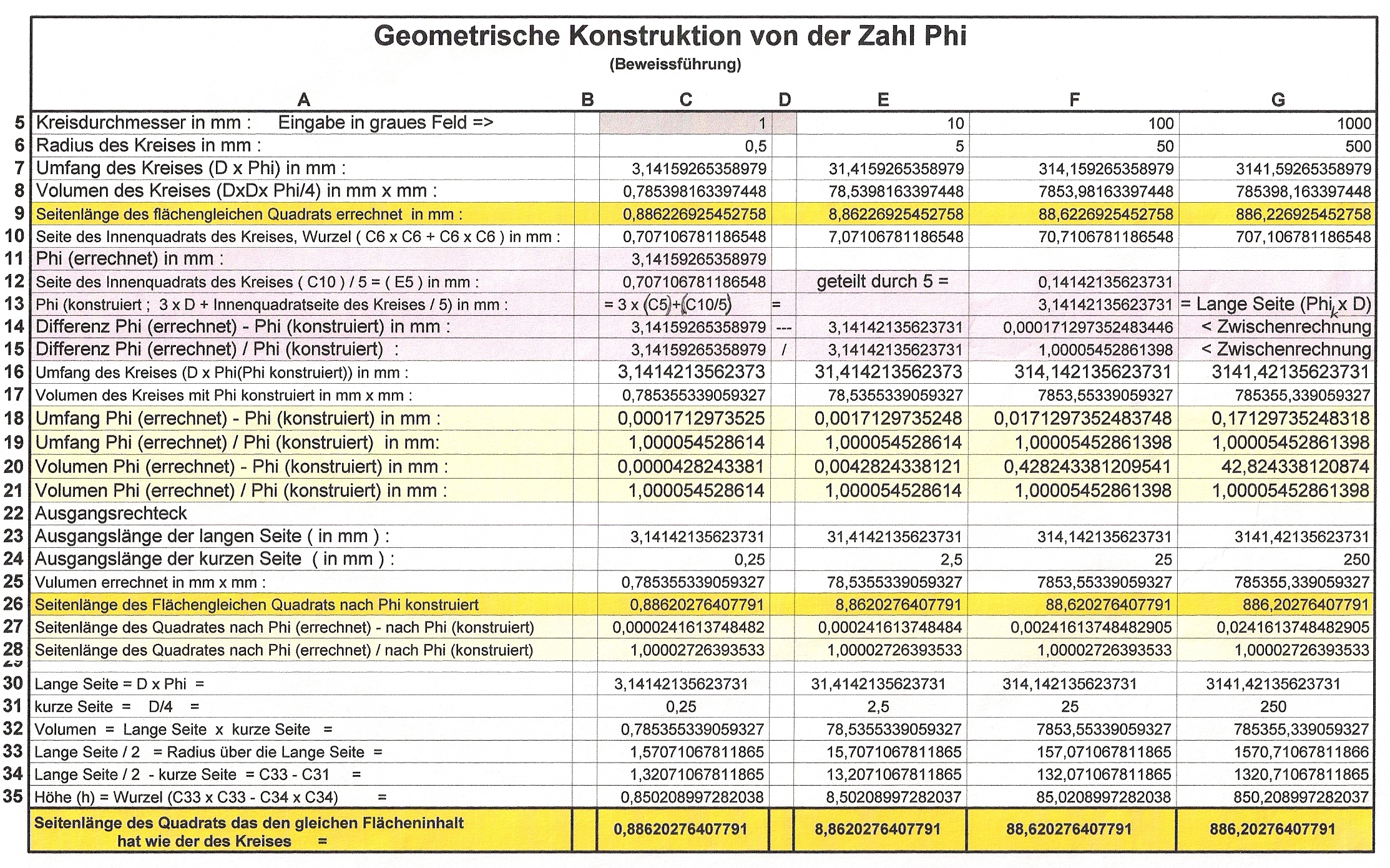
Berechnung

(Auch gibt es eine noch genauere, aber auch aufwendiger Konstruktion. Dazu ist der Autor zu konsultieren.)