Ein Winkel soll in drei gleiche Winkel aufgeteilt werden.

 

Aufgabenstellung:

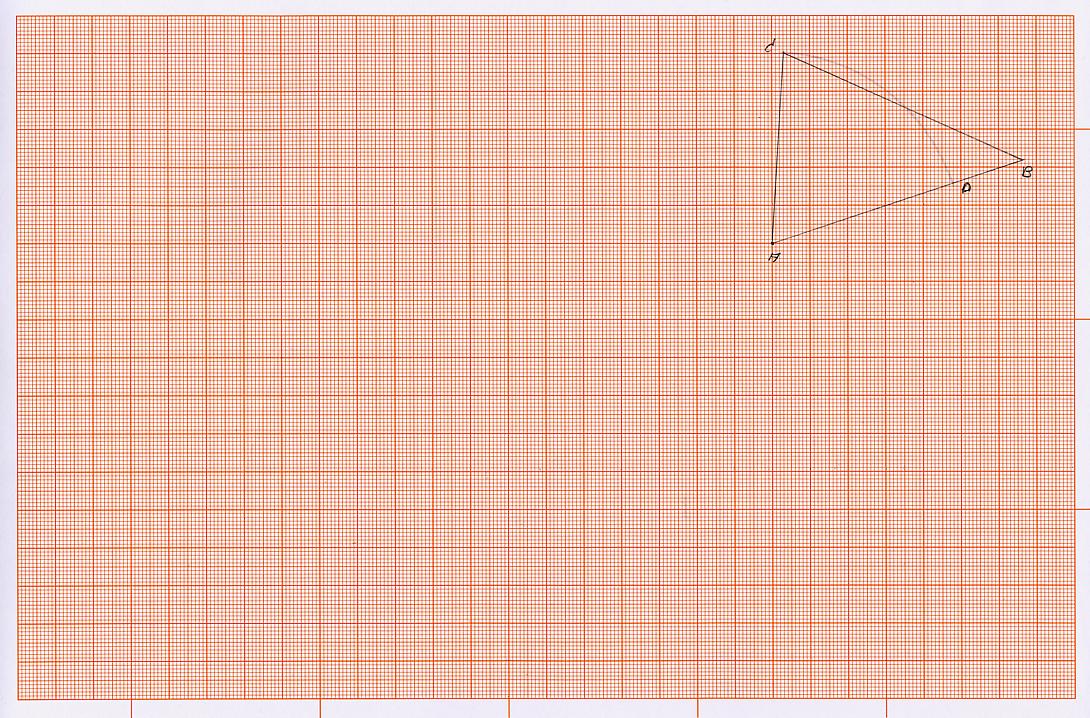
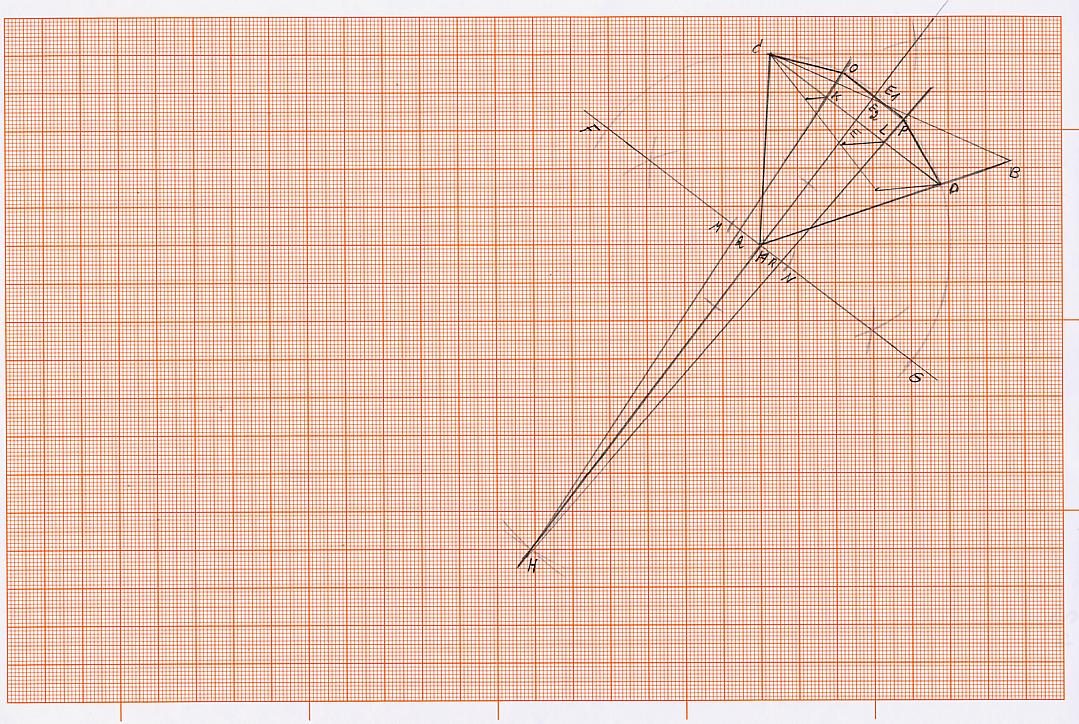
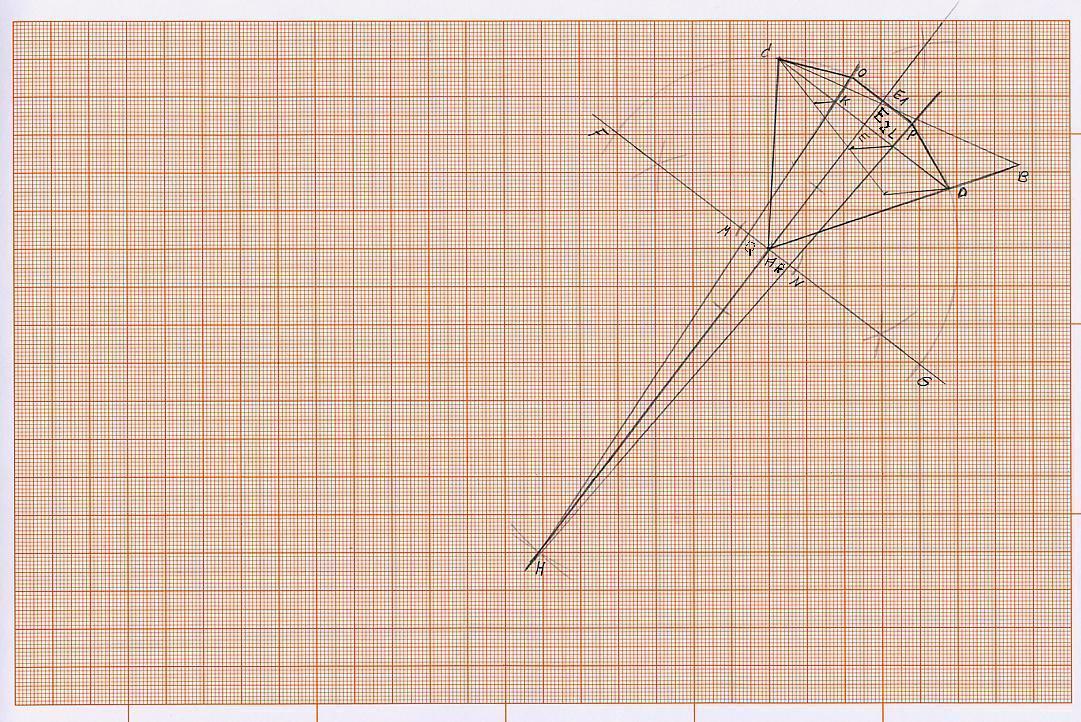
Ein beliebiger Winkel eines Dreiecks mit den Endpunkten A C B soll in drei gleiche Winkel aufgeteilt (zerlegt) werden.

Erkenntnis:

Die drei Winkel sind gleich groß, wenn ihre Sehnen gleich lang sind.

Ausführungsvorbereitung:

Es ist dafür zu sorgen, dass der zu teilende Winkel von zwei gleichlangen Strecken (Schenkeln) gebildet wird. Dazu wählen wir z.B. den Punkt A als Scheitelpunkt für den zu teilenden Winkel des Dreiecks.

Nun schlagen wir um den Punkt A einen Kreises mit dem Radius der Strecke AC (die Strecke AC ist kürzer als die Strecke AB) und schneiden dabei die Strecke AB im Punkt D. Die Strecken AC und AD sind gleich lang.

Es könnte z.B. auch die längere Strecke, also die Strecke AB gewählt werden. Dann müsste die Strecke AC über Punkt C verlängert werden, sodass man dann mit der Strecke AB ein Kreisbogen schlagen kann, der die verlängerte Linie über Punkt C hinaus in einem Punkt z. B. in X schneiden würde. Dann wäre Strecke AX gleich der Strecke AB und somit wäre auch die Forderung, dass der eingeschlossene Winkel über dem gewählten Scheitelpunkt, hier Punkt A von zwei gleichen Strecken (Schenkeln) gebildet wird, erfüllt.

Ausführung:

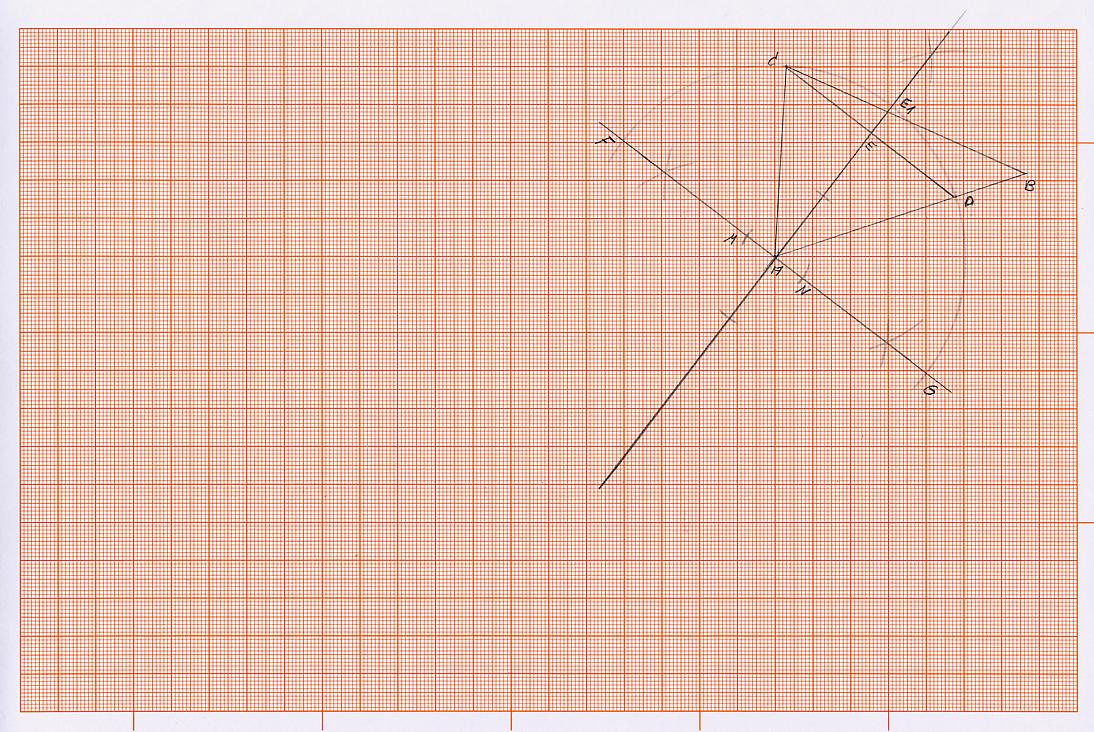
1) Der Winkel (Alpha) gebildet von den Seiten des Dreiecks AC und AD wird halbiert, in dem man

mit einer Zirkelöffnung, die größer ist als der Abstand von Punkt C zu Punkt D, jeweils um die Punkte C und D

einen Kreisbogen schlägt, sodass diese sich schneiden. Nun verbinden wir diesen Schnittpunkt mit dem Punkt A, dabei wird der Kreisbogen, der über Punkt C zu Punkt D führt, im Punkt E1 geschnitten.

Wir verbinden nun die Punkte C und D, dabei wird die Winkelhalbierende im Punkt E geschnitten.

Diese Linie von Punkt A über die Punkte E, E1 hinaus halbiert den Winkel Alpha und somit auch die Strecke AD.

Diese Strecke CD stellt die Sehne unter dem Kreisbogen dar, der mit der Länge AC um den Punkt A zum Punkt D geschlagen wurde.

Diese Strecke ( E zu E1 ) stellt die Höhe (Segmenthöhe oder Kreisabschnittshöhe) unter dem Kreisbogen dar, der mit der Länge AC um den Punkt A von Punkt C zum Punkt D geschlagen wurde, über der Strecke AD. (siehe Skizze).

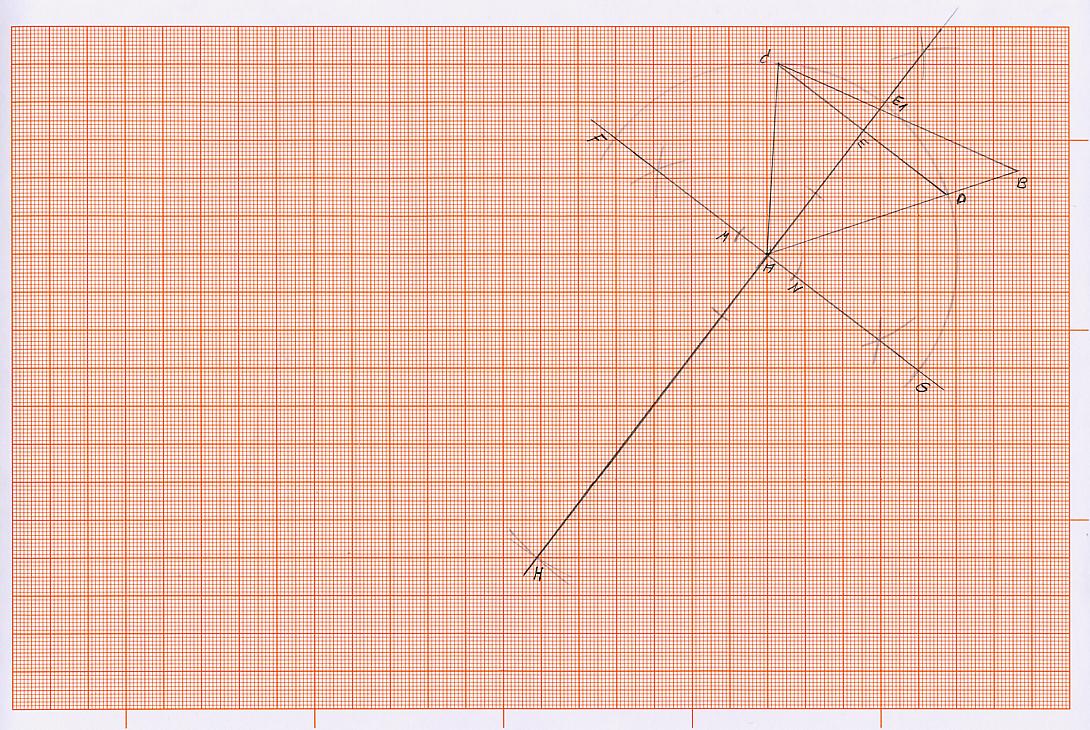
2) Im Punkt A errichte ich nun eine Senkrechte zur Strecke AE, die durch den Punkt A führt, sodass dieser etwa in der Mitte dieser Senkrechten liegt. Dann wird um den Punkt A ein Kreisbogen mit Strecke AC oder AD (beide sind ja gleich lang) geschlagen, sodass die Senkrechte, die in Punkt A errichtet wurde, zweimal geschnitten wird. Der Punkt A liegt in der Mitte der beiden Schnittpunkte, die wir F und G nennen. Die Strecke von Punkt F zu Punkt G steht senkrecht auf der halbierenden Linie des Winkels (Alpha). Wir nehmen jetzt die Strecke EE1 in den Zirkel und schlagen um den Punkt A einen Kreisbogen, sodass dieser die Senkrechte, die in Punkt A errichtet wurde, zweimal schneidet. Diese neuen Punkte nennen wir M und N (siehe Skizze).

3) Wir nehmen jetzt die Strecke FG in den Zirkel und schlagen um den Punkt M und um den Punkt N einen Kreisbogen, sodass dieser die Winkelhalbierende, die über den Punkt A hinaus geht, im Punkt H schneidet (siehe Skizze).

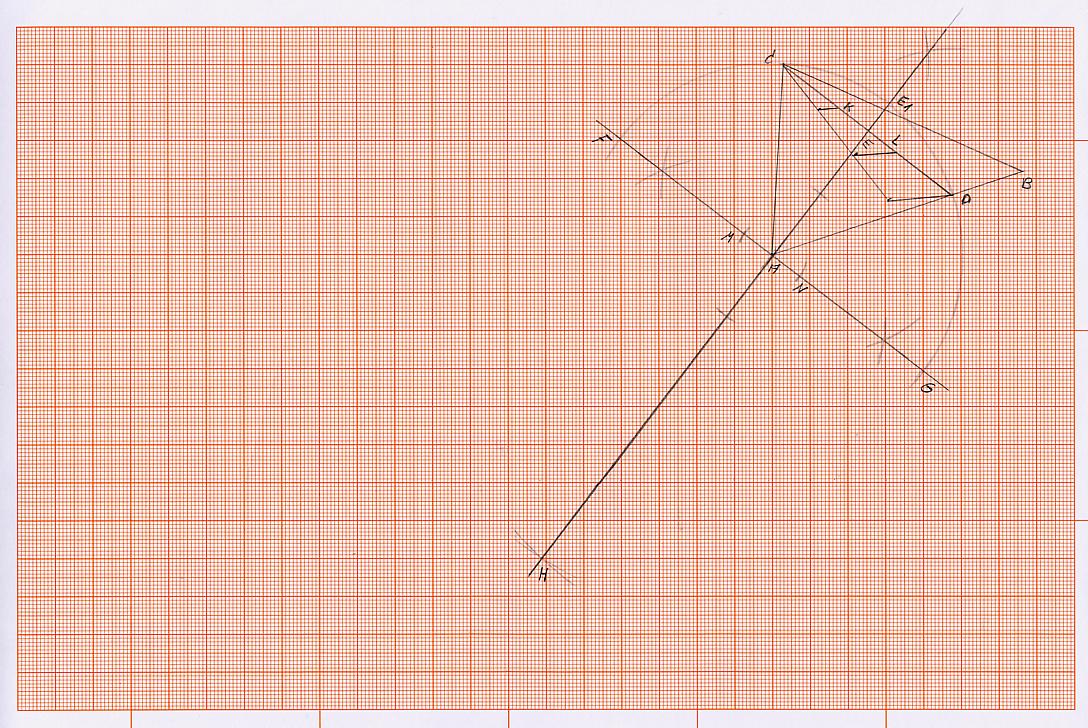
4) Die Strecke CD wird jetzt in drei gleiche Teile geteilt. Dies kann mittels des Strahlensatzes geschehen. Es entstehen 2 Punkte K und L (siehe Skizze).

5) Nun werden zwei Gerade gezogen, die beide von Punkt H aus geführt werden. Eine von Punkt H über den Punkt K und eine von Punkt H aus über den Punkt L (siehe Skizze), dabei werden die Strecken FA und AG in den Punkten Q und R geschnitten. Es entstehen auch auf dem Kreisbogen über die Strecke CD zwei neue Schnittpunkte, nämlich die Punkte O und P (siehe Skizze).

6) Die drei Sehnen auf dem Kreisbogen über der Strecke (Sehne) CD, nämlich die Verbindung von Punkt C zu O, von O zu P und von P zu D sind ziemlich genau gleich lang. Die Sehne OP schneidet die Strecke EE1 im Punkt E2. Der Winkel zwischen den Strecken AC und AO und der Winkel zwischen den Strecken AO und AP und der Winkel zwischen den Strecken AP und AD sind fast gleich groß. Sie haben auch die annähernd gleiche Sehnen- bzw. Kreisbogenlänge. Zur Ermittlung der Strecke (Sehne) OP ist die Hilfslänge E1T rechnerisch zu ermitteln. Sie hilft, dass durch Anwendung des Strahlensatzes, letztlich die gesucht Strecke OP gefunden werden kann.

Somit ist vorgegebene der Winkel Alpha in fast drei gleiche Winkel aufgeteilt.

Die Summe der 3 Winkel entspricht annähernd, mit ausreichender Genauigkeit, dem Basiswinkel (Alpha).

(Zu weiteren Fragen und der Berechnung ist der Autor zu konsultieren.)